Scrappy Jack

iTrader: (2)

Okay, I need a math nerd to help explain a few things in plain language from this white paper:

The Value of Stop-Losses and Stop-Gains in Enhancing Risk-Adjusted Return

It's been years since I even thought about a vector in terms of mathematics and even then, it would have been a cursory understanding. I have a firm grasp on the majority of the document but where I get fuzzy is on page 8. I think I have a reasonable understanding, but I want to be more clear.

I am looking for someone to help explain that section and to:

• give me an idea on what real-world output might look during the various transitions of the stop-loss and stop-gain (aka limit order)
• clarify what the sub-portfolios would look like. For example, are there multiple positions in the stock fund that represent multiple sub-portfolios? Or are there only two sub-portfolios (stock and bond)?
• clarify the level of the stop orders

If you are interested, PM me or post here and I will send you a PM with my email address. Once you've supplied a reasonable response, I'll PayPal you $25. I figure this will take a math nerd less than an hour to read and explain.

Fukalyal

Um, my Dad left his computer on and I couldn't help but notice this page. I've got a fresh pair of diapers on and should be able to type this answer in before bedtime at 7:30. Look at the returns and standard deviations of the various investments on page 8. The stop loss strategy has the highest returns and the lowest standard deviation or volatility. This is because the stop loss strategy is clipping off the highs and lows that would normally drive the standard deviation to the levels found in the other investment instruments, while guaranteeing a high rate of return on gains and fixed rate of loss when it went South. That's not that ******* hard to understand. If I can crawl out of my crib with some effort you can get that if you try.

Real world output would depend on real world input. build yourself some models in Excel with Max/Min settings, run some values through it and watch the output vs an unrestrained model on the same input values. You will see what the other three investment vehicles generated which is unrestrained (unclipped) ranges resulting in the higher stdev numbers; and the unclipped losses lowering your returns in some scenarios.

Dammit I hate when I can't suck my thumb. I'm never wasting four minutes of my life again like this. Keep your money my parents give me everything I need

Fireindc

iTrader: (13)

Fukalyal's son: How does it feel to have a closet father with the forum handle "fukalyal" who hangs out on a miata forum with a bunch of fellow gays?

FRT_Fun

iTrader: (19)

He has a 1.6L m45, he is straight as an arrow. No gay enough for trubo.

Fukalyal

You're asking me what it feels like to hang out here and post amongst the gays? How did you feel seconds after hitting the "send" key? give a kid a break bro

Full gay may have to wait a few years. He's got my college to pay for then I plan to loaf off him for at least 15 years past that.

FRT_Fun

iTrader: (19)

Oh c'mon how much does community college really cost.

Scrappy Jack

iTrader: (2)

Hi. Thanks for your attempt at a condescending, smarmy reply. I was about to write a scathing response about how you completely ignored my initial request. I was about to quote some specific elements from page 8 (like "Each sub-portfolio k 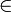K, has a unique stop-loss and stop-gain level represented by a two-dimensional vector, δk = (αk , βk)." [Note the variable k in the previous formula should be subscript.]

Imagine my surprise when I realized the author had updated the paper on the 7th of July (my copy was dated 2013-07-02) and that page 8 now includes the basic output. I am clear on the generic outcome of the paper and understand the information presented on the current page 8. My question has to do more with the specific details of the outputs on the current pages 4-6.

I'll have to read through the current version as I already see some changes from the version I was working through.

I'll try this but I'm not sure I have a strong feel for the specific Excel function to be used. As I understand it, there are 4 stops and 4 limits used, with the fixed spread between them being 0.5.

The paper reads, "The length N vector of possible investment assets, S, must also be specified." That is saying that N = the number of asset classes (in this case stocks and bonds, N=2)? And S is the designation for each one, differentiated via a subscript?

Given an I of 4 and J of 4, the result is 16 different sub-portfolios. I'm having a little bit of a hard time visualizing that but maybe some time in Excel will help solidify my understanding.

Fukalyal

Well the good thing is you didn't take it wrong. If you weren't so self absorbed with your own problems you migh have some concern for others for example do you have any idea how difficult it is to impersonate a toddler. I wasn't very good at it or the math either and now I feel bad. I will read through this paper a little more as the subject matter is certiainly interesting and everyone can gain from a little investment strategy.

My problem with papers like this and tons of stuff in academia is these authors will use the absolute maximum of their skills and education when trying to explain something, almost as if the KISS theory has completely escaped them. Or the paper is a walking advertisement for their next grant, if it was easy to understand they wouldn't be needed. The only place I have found a real use for excessive detail is fluid dynamics or FEA analysis that encompasses thermal, material, mechanical stresses to simulate distortion with consideration of all phyiscal properties. But maybe that's just the knuckle dragging mechanical guy in me.

Either way thanks for posting this problem because the approach being promoted can be used by almost anyone with a brokerage account. It strikes me as a very detailed way to implement stops both for gains and losses for the purpose of limiting volatility. Although I'm no sure what the point is of limiting gains on the high end, will have to examine that a bit more.

Scrappy Jack

iTrader: (2)

In generaly, I agree with you. That's a big part of why I wanted to better understand the methodology.

That's part of why I posted it here. Besides being willing to compensate someone for their time and effort (rather than just asking for free help), the nominal dollar amount could be compounded with possibly practical knowledge. That is, someone helps me translate the math nerd jargon in to plain English and they get $25 plus a possibly useful tool for their own personal investments.

The point of the limit orders (with the stop-losses) is a modified, quantitative version of asset allocation rebalancing.

3rdCarMX5

iTrader: (1)

Have to love when authors use jargon to try and elevate the subject matter. As a simple equation or a algorithm it all makes sense, but the papers are almost unreadable without a current textbook or a pubmed account.